志望校対策は、模試での判定結果、偏差値の壁を越えて、 合格を掴み取るためには欠かせない手段です。それは時に劇的な効果を持つ魔法のようなものとして謳（うた ）われます。しかし、志望校対策の実態とは、指導教員が実際に志望校の過去問を最低でも5年分以上を解き、 志望校の過去問の傾向を紐（ひも）解く地道な努力の積み重ねです。またそれらの分析結果を踏まえた上で生徒に向き 合い、「教え子はどの問題が解けないのか」「それはどういう思考過程を踏んでいるからなのか」、「その思考過程を 修正するために、何をアドバイスしてあげられるか」を考えていくことになります。毎回の授業を通して行われる生徒 との対話、修正こそが志望校対策の本質になります。

私達は、将来の日本を背負って立つ可能性あふれる子供たちの、重要な教育を任されており、中学受験はまさにお子さんの大切な進路を決定するものになります。また、お子さん本人の努力はもちろんのこと、お子さんの学習環境を支えてこられた周りの人々の想いが結果として実るように、志望校対策には万全を期して望んでいます。

　中学受験の成功と失敗の定義とはもちろん結果によってのみ判定され、志望校に合格することが成功であり、 不合格になってしまうことが失敗であると言えます。合否の分かれ目になっているもの、それは合格最低点です。つ まり、「成功＝合格最低点を１点でも上回ること」であり、逆に「失敗＝合格最低点を１点でも下回ること」と定義 できます。志望校が決まった場合、必然的に志望校の合格最低点という目標点数と、試験日程から逆算して期日が 決まることになります。志望校対策では、 目標と現状の差を埋める戦略・点数をどのようにあげていくかという具体的な戦術を考えていかなくてはなりません。

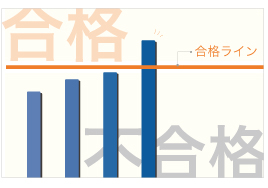
ここでは具体的に分かりやすくするために、志望校の4科の配点は傾斜配点であり、 算数100点、国語100点、理科50点、社会50点の計300点満点であるとして話を進めます。

　はじめに、ここでの目標の合格最低点の設定とは、「この点数を取れば合格することがほぼ確実な点数」を決めることを指します。 合格最低点には当然ながら年次ごとの受験生のレベル・問題の難易度において多少上下があります。 教師であれば年次ごとの問題の難易度を把握した上で合格最低点を設定できるのですが、ここでは参考までに一番簡単な設定方法を示しておきます。

”低すぎず、高すぎず”が重要です。もちろん合格最低点の設定は高ければ高いほど、合格はほぼ確実にはなりますが、 むやみやたらと高く設定することはひかえましょう。ここでは仮に志望校の合格最低点が180点（6割）であったと仮定します。
ここで注意しておきたいことは、目標として採用した合格最低点はとは取れたらいいな、という希望観測的な点数ではありません。 ]目標の合格最低点という言い方こそしていますが、それはかならず実現させなければならない数値であり、それを1点でも割れば、志 望校に合格できないという意識をもって捉えることが重要です。

　次に、現在の実力を把握しましょう。志望校の過去問を1年分解いたところ、計130点（算数30点、国語50点、理科20点、社会30点） であった仮定します。ここで初めて問題意識、明確な問題設定ができます。

　これで、ようやく志望校対策の第一歩を踏み出せます。志 望校に合格するためには、残された期日で、この残りの50点をほぼ確実に取れるような実力に仕上げていく事が必要なのです。

　STEP1で50点あげることが必要であると分かりましたが、それだけではまだ目標は不明瞭です。 どの科目で何点あげるのか、もっと具体的に把握していかなくてはなりません。まず、目標の合格最低点が6割ですので 、理想の取り方は各教科6割を割らなければよいわけです。この場合4科の目標点数は各教科の満点に6割掛けしたものになります。 そうすると、以下のように、各教科の足りない点数が出てきます。

　この方法が最もシンプルで、わかりやすい各教科の目標点数の算出方法です。 しかしこれだけでは２つの要素（試験の難易度・お子様の得意/不得意）が欠けていますので、ここか ら4科の配点の微調整が必要となります。「大まかな理解だけでかまわない」とい う方は次のSTEP3に進んでくださって構いません。各教科、点数の微調整において考慮すべきポイントを、重要な順に列挙します。

　最後に考慮しなくてはならないことは、受験までの期日は限られているということです。残された時間で、ど の時期にどの教科を意識的に伸ばしていくのかということを計画的に決めておきましょう。 残された時間のうち、多く時間を割かなければならない科目の決め方の基準は以下のようになります。

　目標点との乖離が大きい教科を優先的に対策するようにしてください。上記の 例ですと、優先的に対策しなければならない科目は、1番目に算数、2番目に国語と理科、3番目 に社会になります。つまり、得意な科目を伸ばすのではなく、苦 手な科目を克服することを優先しなくてはならないというわけです。当のお子様にとっては頭の痛い問題ですね。

　基本的に目標点との乖離が大きいものに優先的に時間を配分すれば大丈夫です。先ほど、2番目に対策すべき科目は国語と理科と挙げましたが、傾斜配点を考慮すると、理科より国語のほうが優先的に対策する科目となります。なぜなら国語で10点あげることと、理科で10点あげるときに費やす労力は一緒ではないからです。それぞれ10点をあげるのでも、国語では1割分の実力アップでよいのに対して、理科では2割分の実力アップが求められます。言い換えると、100点満点のテストで10点をあげることより、50点満点のテストで10点を上げることの方が難しくなります。 　近年算数・国語：理科・社会＝2：1という傾斜配点は減ってきていますが、傾斜配点の持つ重要性については十分に認識しておく必要性があります。傾斜配点が2：1の場合にはその重要性はいくら強調してもしすぎることはありません。

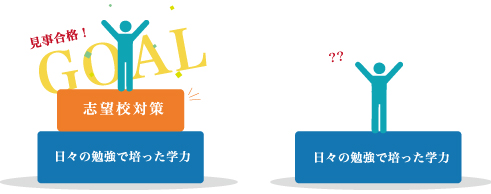
　志望校対策は受験の総仕上げに当たる部分です。集団指導の塾のカリキュラムだけで は志望校対策まで十分な指導をすることができないということは前述したとおりです。ここでは野 球の比喩を使って、過去問分析がどのようなものかを説明します。野球選手は毎日、ランニングや素振り などの練習をして技術の向上に努めていますが、それだけでは十分ではありません。最後に必ず、対戦相 手のピッチャーのデータを頭に入れて打席に立ちます。ピッチャーがどんな球種をもっているのか、どう いう順番に投げてくることが多いのか、どの球種に狙いを絞るかなど…日常の鍛錬の上に最後は対戦相手 のデータを踏まえて実戦に臨む事になります。 　過去問分析はこの対戦相手の分析をし、対戦相手に特化して技術を仕上げる部分に当たります。注意 としては、今まで全くバットを握ったことがない人に、対戦ピッチャーのデータだけ与えても打てるわけ がないのと同様、中学受験の志望校対策も日々の学習によって築かれた学力という土台があってはじめて機能することになります。

志望校によって対策は大きく異なってきます。入試問題との相性によって、志望校の変更を考えるご家庭もあるほどです。ここでは算数を例に紹介します

　男子校と女子校を比較すると、両者の対策は全く異なったものになります。男子校は特定の限られた単元から、難しい問題が一定量出題されるのに対して、女子校は幅広い単元から標準的な問題が多量に出題される傾向にあります。しかし、これらはもちろん一般論であり、女子校でありながら男子校のような出題をする学校（鷗友学園はその代表格）もありますので、やはり最終的には全ての学校を個別に分析していくしかありません。
各学校の出題には特徴があります。伝統的に受け継がれてきた出題のようなものも見受けられます。共立の概算などの実用的な算数、芝のダイヤグラム・平面図形問題、開智・巣鴨の立体に対するこだわりなど…挙げはじめると切りがないですが、各学校の特徴が明確に出ています。また出題構成においても違いがあります。青山学院のように終始淡白な出題（全体的に難易度の高低が少ない）もありますし、吉祥女子のように明確に誘導形式の出題（段階的に難易度が上げられていく）をする学校もあります。出題内容・構成から出題者の意図を読み取り、受験校ごとに対策を立てることが非常に重要になります。好まれる単元や出題構成などを分析していくと、１問あたりにかけられる時間や、目標点数を取るために取るべき問題と捨て問がどこにあるかなど、細かい戦術を立てることが可能になります。
志望校対策が最上位校からどんな学校に至るまで、有効に働くことは事実です。どの学校も過去問を解いていけば、その学校で求められている力を読み取ることは可能です。しかし、強いて言えば志望校対策が最も有効にはたらく学校は、オーソドックスな出題が多くを占める最上位校を除いた学校ということにはなるでしょう。最上位校においても志望校対策はもちろん有効です。基本的に学校の偏差値が上がるほど、対策する範囲が広くなったり、出題される単元が数の性質や平面図形というように分かっていても、自由度が高い問題（例えば麻布中学校の平面図形）が出題されることが多くなります。要求される力がより抽象的になっていくようには思います。複雑な連立方程式の取り扱い、数の性質・図形問題に対する高度なセンス、場合の数に対する臨機応変な規則性の発見…といった具合です。このような出題の場合には、今までの演習量で得られた経験や直観が幅を利かせる部分が多くなります。これらの問題には類似問題を多量に演習することによって対応していきます。（ただし上位校であっても女子学院、慶応普通部のように典型的な問題を素早く処理することを求めている場合には、具体的な対策はしやすくなります。開成や早稲田中学校も、簡単ではないもののオーソドックスな問題から大きくそれない傾向にあります。）

　この項目では分かりやすく説明するために、算数を例にして具体的に述べましたが、各学校、教科ごとにそれぞれに特色があります。過去問分析では、志望校の出題の特徴を把握することに努めましょう。

過去問分析をもっと見る

過去問分析をして志望校の出題傾向を知り、お子さんの得意・苦手な単元を把握すると、すべての単元を次の４つの象限にわけることができます。（右図）
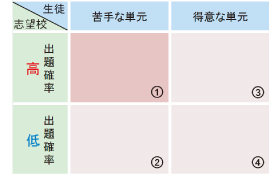
①出題確率が高く、お子様が苦手な単元
②出題確率が低く、お子様が苦手な単元
③出題確率が高く、お子様が得意な単元
④出題確率が低く、お子様が得意な単元
　最優先的に取り組まないといけないのが、①「出 題確率が高く、お子様が苦手な単元」です。 4科全てにおいて、設定した目標点に達するまで、 1つずつ丁寧にこの単元を克服していきましょう。 これこそが、最も確実で、点数の伸び幅が期待で きる勉強法です。全分野を満遍なく勉強する模試 対策とは全く違い、志望校対策とは入試問題と向き合いしながら、自分のできない問題を一つずつ克服していくことを指します。”敵を知り己を知れば百戦危うからず”です。 　特長でも紹介しましたが、修明塾では志望校の出題傾向を踏まえた上で、毎回の演習を通して生徒の 得手・不得手と向き合い、入念に志望校対策をしていくことになります。私達中学受験のプロは単元と その解法を、頭の中に整理して収納していますので、それぞれの生徒に必要な問題を選別し、苦手分野を克服させていきます。